Investigation of fading between DCF39 (

Investigation of fading between DCF39 (Burg) and CT1DRP (Porto)

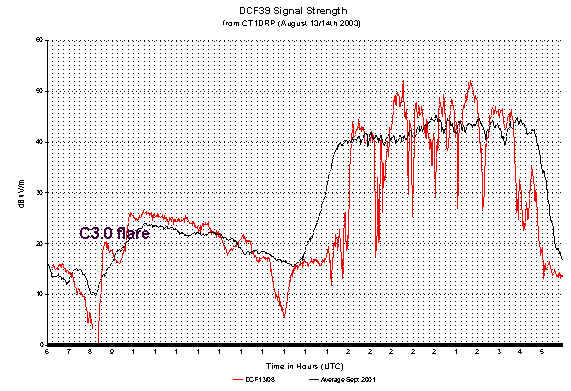
A plot of the signal strength of DCF39 ( a German Utility station on 138.83kHz) taken by Brian CT1DRP at Porto on August 13/14the 2003 set me thinking about the mechanisms of the deep narrow troughs produced in the plot. I surmised that these were probably due to the two-hop signals and the one-hop signal interfering ( in the optical sense ) destructively. I have advanced this idea on a number of occasions but never had any hard facts to back up my hunch. Looking carefully at the plot I saw that the troughs were some 20dB below the mean signal level, and it occured to me that this would mean that the signals on the two paths were within 1% of the strength of each other. This was a little surprising at first as I had always believed that the two hop signal would be subject to more attenuation because of its two passages through the D-layer, to a reflection level thought to be around the base of the E-layer. These thoughts encouraged me to polish up my school algebra and make some simple calculations on path differences to see if the figures would support my ideas.

To my mind the plot above indicates that the the night-time level is determined by the interaction of predominantly just two paths. I have constructed a "naive" model of the ionosphere where I consider that both paths are "reflected" from the same level in the ionosphere. The action at the ionosphere is treated as a mirror-like reflector. This is NOT what happens in practice, but it will suffice for a calculation to indicate the magnitude of the effect. The maths involves some fairly simple algebraic geometry, and hopefully is not too difficult to follow. The panel below describes the derivation of the equations for the slant-path lengths of the one-hop and two-hop signals.

I did start to try to reduce the formulae but decided instead to evaluate them in an Excel spreadsheet. I also calculated the phase difference in degrees between the two paths. This indicates that a movement of the reflection level (on this simple model) of between 4 and 6 kms in altitude would produce an sufficient phase change to cause the two paths to interfere destructively. If we also consider the time difference between the troughs (60 to 75 minutes) we can calculate the velocity of the movement of the reflecting layer at 60 to 90 m / minute. The graph below is evaluated at 500m intervals of altitude. If it was done at a smaller interval the trace would go right to + /-180 degrees.

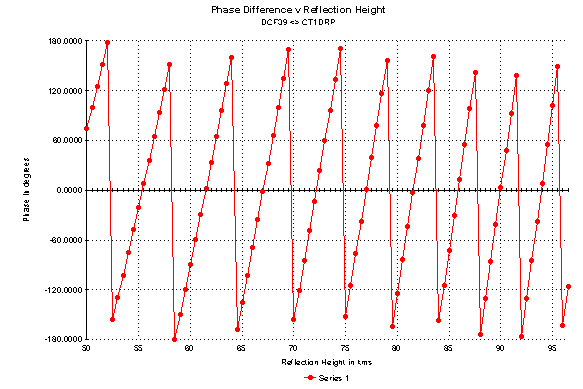
I believe the figures support the plausibility of the one-hop/two-hop interference explanation. There are many other factors that would have to be taken into account in the real-world situation. The higher angle two-hop signal would probably penetrate deeper into the ionosphere, than the more grazing-angle one-hop signal. Thus the reflection height would not be the same for both paths. The "return" of the signal is by refraction and not by mirror-like reflection, thus the two-hop signal may spend an appreciable time in the ionosphere aquiring sufficient diffraction to return earthwards. The two "reflection" points for the two-hop signal are 1000kms apart and may be at different altitudes.

The spreadsheet will also allow the position of the "interference" fringes on the ground to be estimated. It occurs to me that if another station receiving a predominantly ionosheric signal from DCF39 were to record a trace of the strength similar to Brian's it might be possible to calculate the actual height of the "reflecting layer". Unfortunately most of us live too close to Burg !! Up to 700kms distant the ground wave predominates even at night-time. At the distance of 1950kms of CT1DRP the groundwave component is very weak, which is why we can see "skywave" enhancement in the day-time.

Further thoughts

My initial thought was that the path differences might be caused by slow decay of the precipiated electrons, allowing the "reflection level" to rise slowly during the night. A quick count of the number of peaks and the probable thickness of the D-layer suggests that this is not a good model. If it were, then the whole of the excess ionisation would have decayed in one night and we know it did not.

Another possibility is that the level of the reflecting layer is oscillating. I believe that there is some support for this model in my observations. One can imagine that after the asymmetric shock of a collision with a CME, the ionospheric "shell" will not just return to its normal state, but will "ring". It is a complex loosly bound structure and so it will probably oscillate with a wide range of frequencies. Some of these may be "overtones" and like on a musical instrument may well die out before the the more fundamental oscillations. This could explain the rapid but relatively shallow "flutter fading" I observe soon after a geomagnetic storm. These rapid fades seem to die away night by night leaving the slower "oscillations" which seem to drop in frequency as the storm "after-effects" die away.

If this is the case the lengthening fading pattern is not an indication of the progress of the recovery but more a measure of the time since the ionospheric shell was "tweaked". It may still provide a useful indication of the likely occurence of some slow constructive interference which will enhance the received signal levels.